Моделирование АЦП с использованием полинома интермодуляции и эффективного числа бит

В этой статье мы обсуждаем другую методологию моделирования АЦП в системном моделировании, на этот раз с использованием эффективного числа битов, а также с настройкой нашего АЦП. вводя полином 5-го порядка на вход идеального квантователя.

До сих пор в этой серии мы обсуждали достоинства различных способов моделирования преобразователей данных в системном моделировании, в частности, с использованием метода моделирования с использованием эффективного числа битов или ENOB.

Теперь мы продолжим это обсуждение, добавив новый элемент:корректировку нашей модели АЦП напрямую с помощью полинома 5-го порядка, добавленного к входным данным идеального квантователя.

Описание нашей новой модели АЦП

Модель, представленная в нашей предыдущей статье, не дала никаких отчетливых паразитных частот (паразитов). Поскольку паразиты являются важной характеристикой производительности АЦП, потребовалась лучшая модель.

Это показано на Рисунке 1.

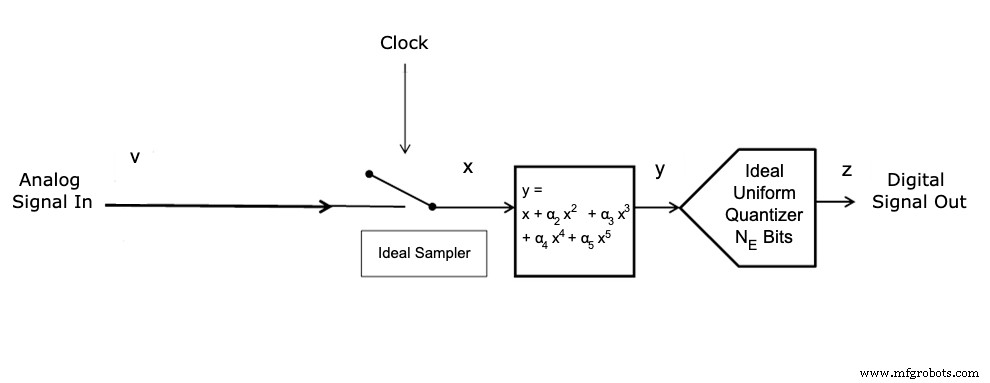
Рисунок 1.

Это добавляет полином 5-го порядка к входу идеального квантователя.

Двухтональный вход следует использовать для определения параметров α _i (f _c ) и N _E (f _c ); где f _c - это центральная частота между тонами, как показано на рисунке 2 (который вы узнаете на рисунке 4 из нашей первой статьи).

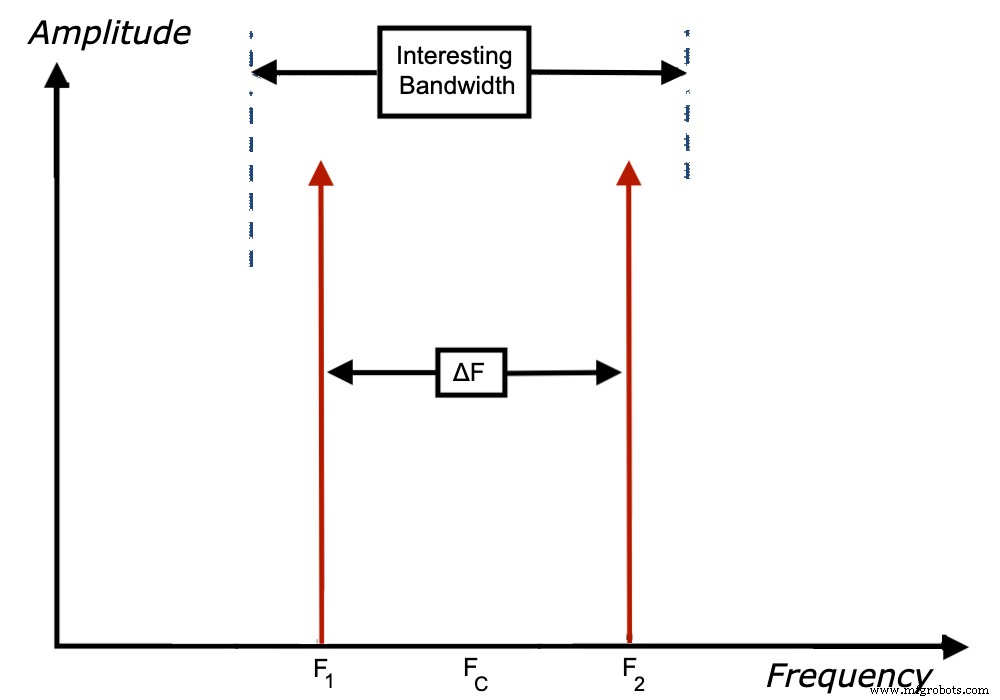
Рисунок 2

Если какой-либо из этих параметров также является функцией Δf, разделения между тонами, вероятно, существует нелинейность с памятью в АЦП, и эта модель не будет применяться.

В качестве примера использовался тот же двухтональный вход, как показано на рисунке 3 (обсуждаемый на рисунке 3 из нашей предыдущей статьи), с N _E =8 бит, α ₃ =0,04, а все остальные α _i =0. Существуют та же полоса пропускания Найквиста (730,9 МГц) и «интересная полоса пропускания» (233,7 МГц), что и в нашей предыдущей статье.

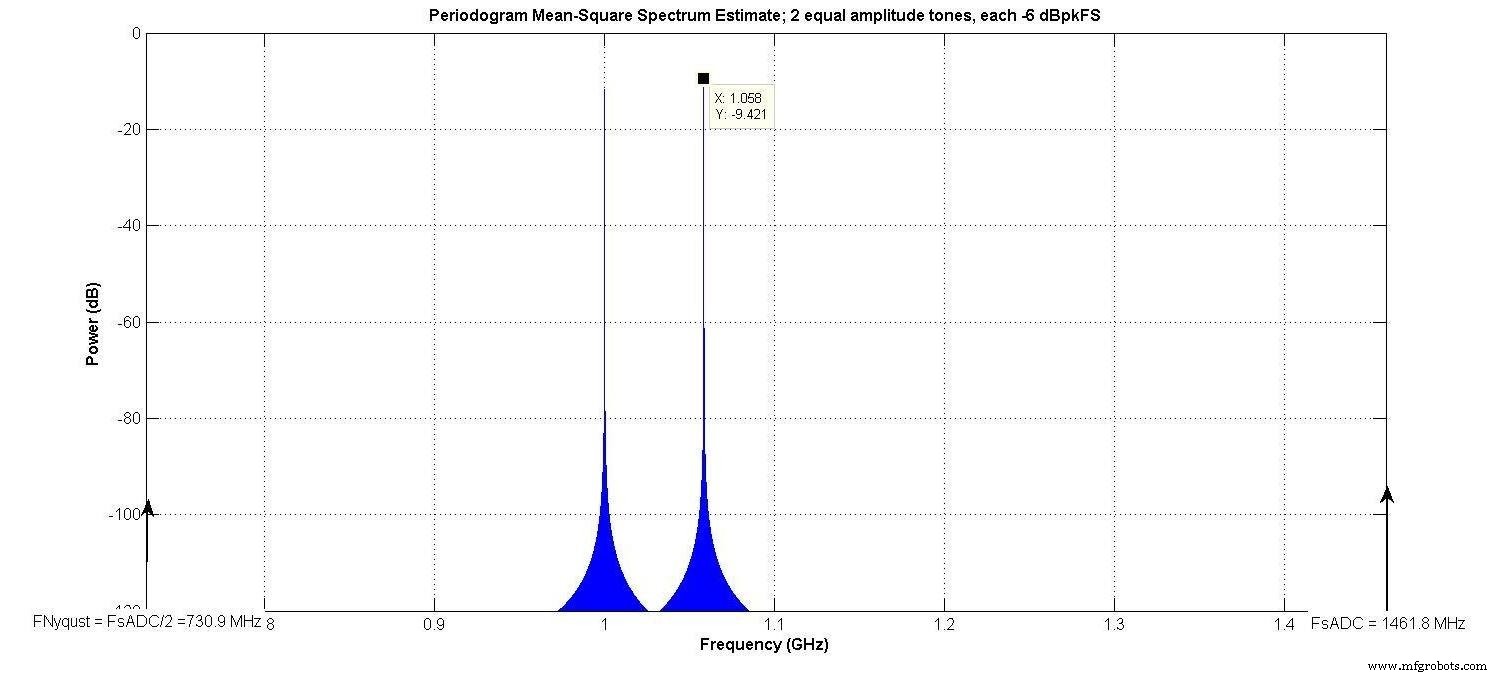
Рисунок 3

На рисунке 4 показан выход с однотональным входом, а на рисунке 5 показан выход с двухтональным входом.

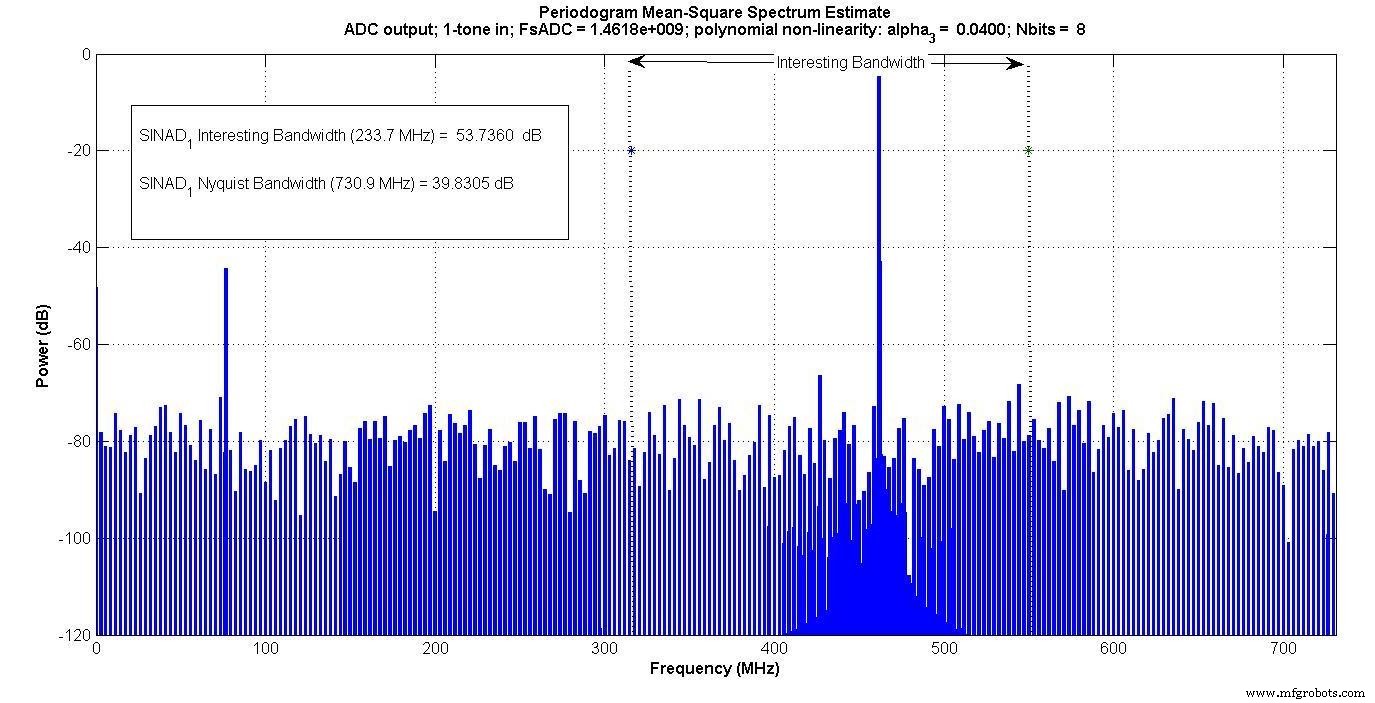
Рисунок 4.

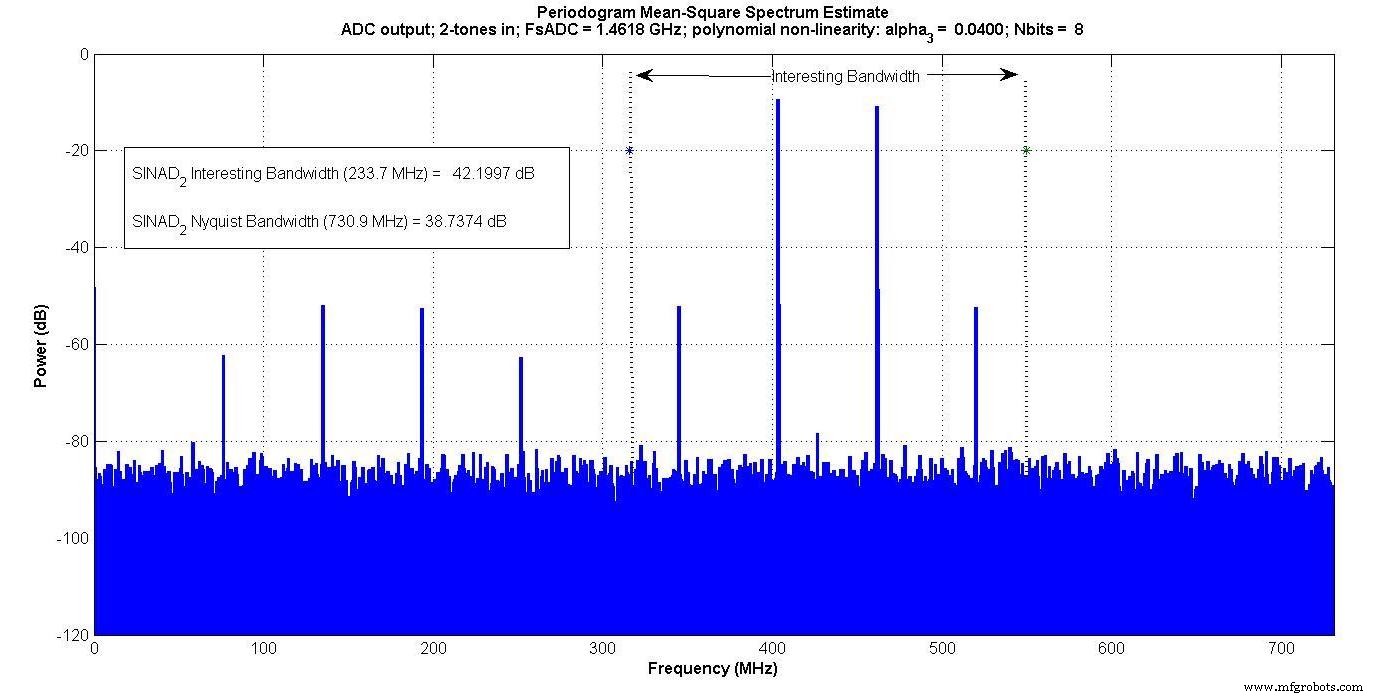
Рисунок 5

Продукты интермодуляции появляются внутри «интересной полосы пропускания» для двухтонального входа, но не для однотонального входа.

Если бы кто-то измерял только в этой «интересной полосе пропускания» - например, если бы был цифровой полосовой фильтр, который пропускал только эту полосу - однотональный тест не улавливал бы эффект интермодуляции, а двухтональный - бы.>

На рисунке 6 показаны различные SINAD для 5–12 входных битов. Очевидно, что однотональный вход, измеренный в «интересной полосе пропускания», не улавливает эффект интермодуляции для более чем 7 бит.

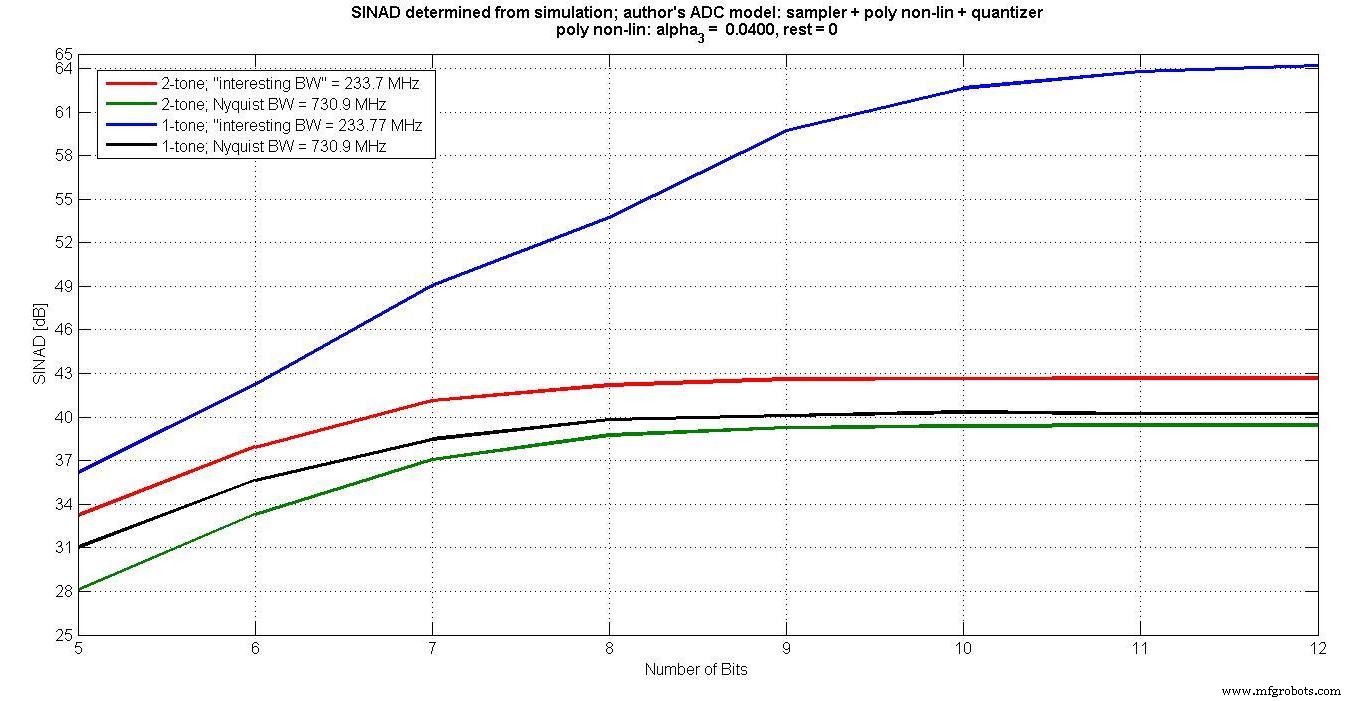
Рисунок 6

Кроме того, для более чем 7 бит, поскольку шум квантования уменьшается с увеличением количества бит, но интермодуляционные искажения остаются прежними, SINAD не улучшается с увеличением количества битов.

Сравнение с моделью производителя

Дорогой читатель! Теперь вам может быть интересно; "Ну и что? Это всего лишь некоторые модели и их ответы на некоторые сигналы. Какая цель? »

Цель должна заключаться в том, чтобы двухтональные измерения можно было проводить на АЦП, а значения параметров, показанные на рисунке 1, выбирались так, чтобы они наилучшим образом соответствовали измеренному выходному сигналу АЦП. Часто это можно сделать вручную, отрегулировав их до тех пор, пока не будет получено хорошее прилегание. Затем упрощенную модель можно использовать в симуляциях с большим коэффициентом битовых ошибок (BER).

Измерения могут быть выполнены на реальном устройстве, на хорошей модели устройства или взяты из технических характеристик производителя.

Чтобы быть хорошей моделью, она должна максимально приближаться к реальному устройству; например, полная модель SPICE. Выполнение такой сложной модели в моделировании BER займет слишком много времени.

Вашему автору было предоставлено производителем то, что они назвали «поведенческой» моделью, которая, как они утверждали, охватывала все важные параметры конкретной модели АЦП. Модель производителя также учитывала как внутренний, так и внешний джиттер часов. Это было использовано для оценки метода.

Двухтональный ввод

На рисунке 7 показана схема моделирования. Был сгенерирован двухтональный входной сигнал, который затем был введен как для модели вашего автора, так и для модели производителя. Оба были отображены со спектральным анализом.

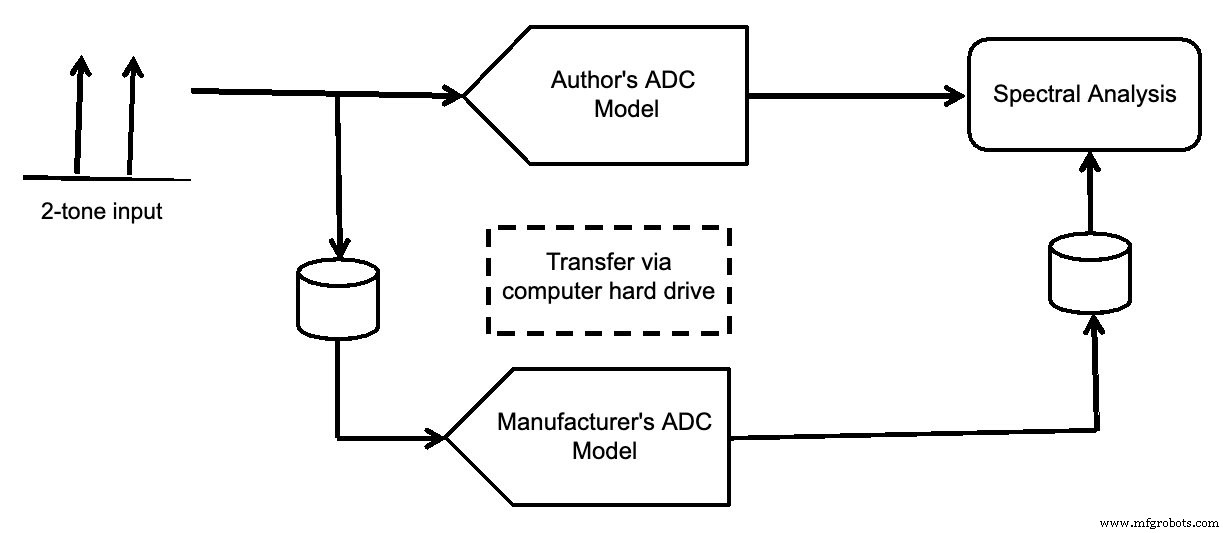
Рисунок 7.

На рисунке 8 показан используемый вход. Два тона находятся в диапазоне от 300 до 350 МГц. Частота дискретизации АЦП составляет примерно 250 МГц, поэтому эти тона находятся в 3-й зоне Найквиста.

Так как каждый из них имеет пиковое значение -6,02 дБпик, когда они добавляют синфазно, напряжение будет вдвое больше, в результате чего будет 0 дБпикFS.

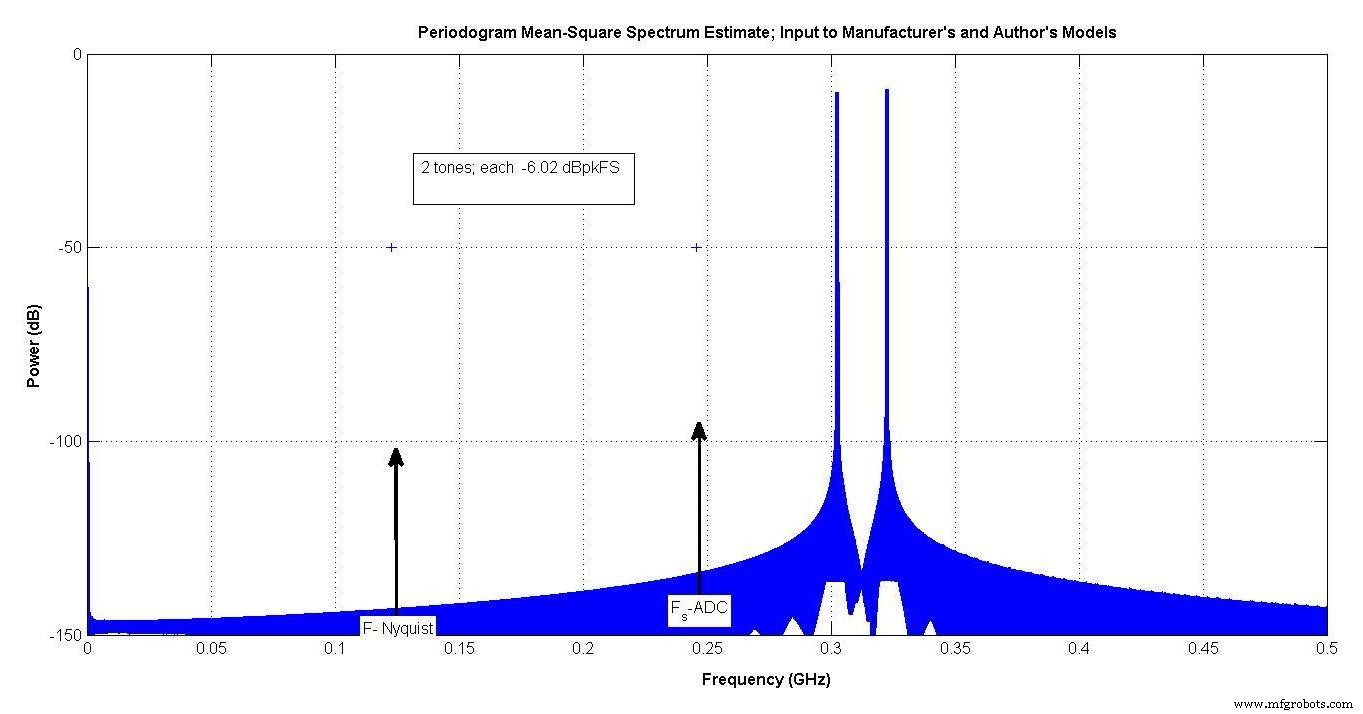
Рисунок 8

На рисунке 9 показаны выходные данные модели производителя, у которой SINAD составлял 63,74 дБ в «интересной полосе частот» примерно от 27 до 107 МГц.

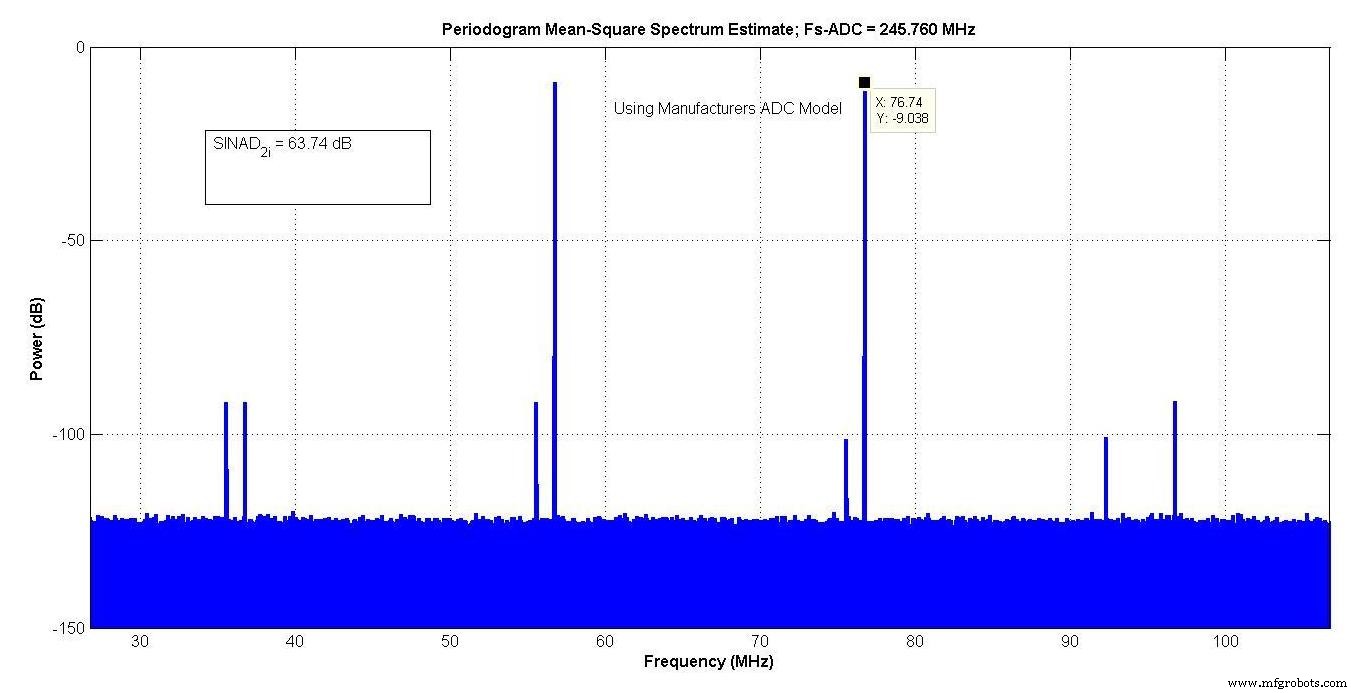
Рисунок 9.

На рисунке 10 показан результат после настройки параметров модели вашего автора для соответствия.

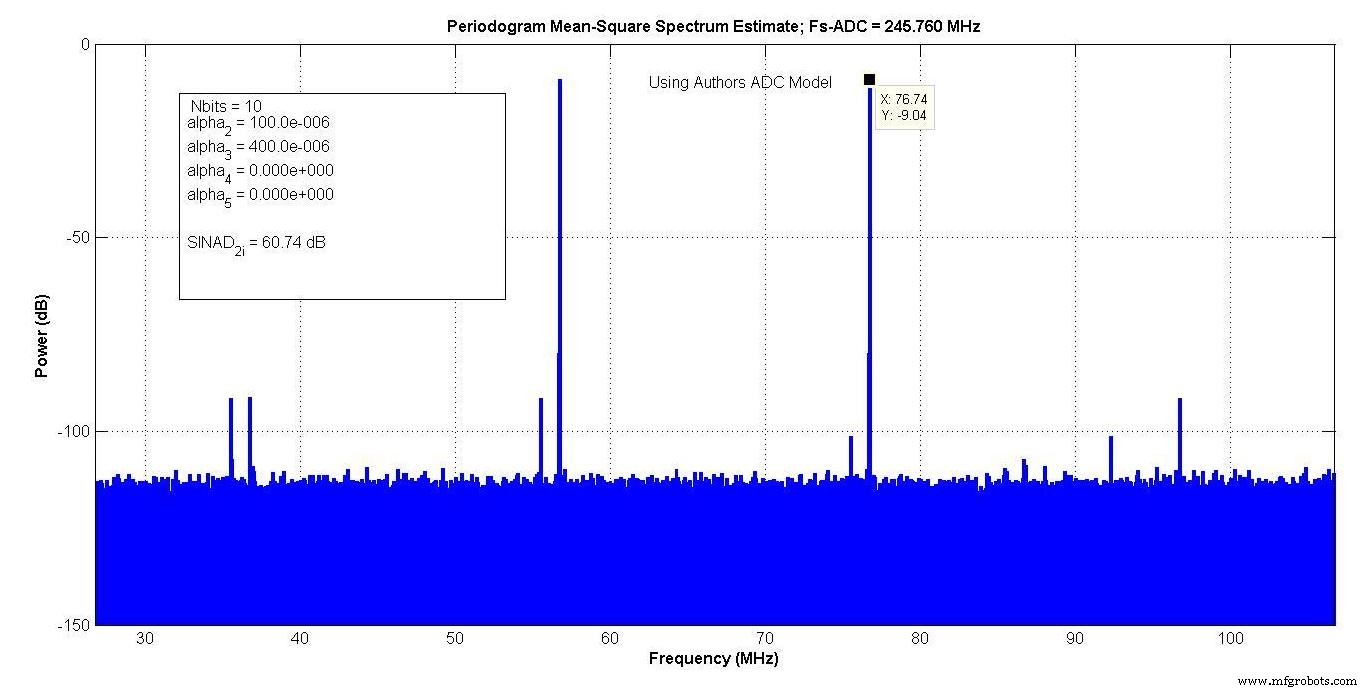
Рисунок 10.

Коэффициенты полинома давали достаточно степеней свободы, чтобы можно было почти точно сопоставить шпоры. N _E 11 бит давали минимальный уровень шума на 3 дБ ниже, чем у модели производителя, а N _E 10 бит давали на 3 дБ больше, чем у модели производителя.

Ваш автор решил использовать пессимистическое значение 10 бит, что дало SINAD 60,74 дБ. Усовершенствованная модель позволит добавить до 6 дБ аддитивного белого гауссовского шума, поэтому более высокое значение N _E можно было бы выбрать, и добавить дополнительный шум, чтобы соответствовать минимальному уровню шума.

Входной сигнал OFDM

Эти две модели теперь можно сравнить с сигналом связи на входе.

Имеющийся в продаже программный пакет поставляется с моделью LTE; который генерирует сигнал OFDM. Модель включает в себя модулятор, частотно-избирательный канал с рэлеевскими замираниями, аддитивный белый гауссовский шум и демодулятор.

Можно вставить модели АЦП перед демодулятором и оценить спектр выходного сигнала АЦП и величину вектора ошибки сигнала OFDM, как показано на рисунке 11.

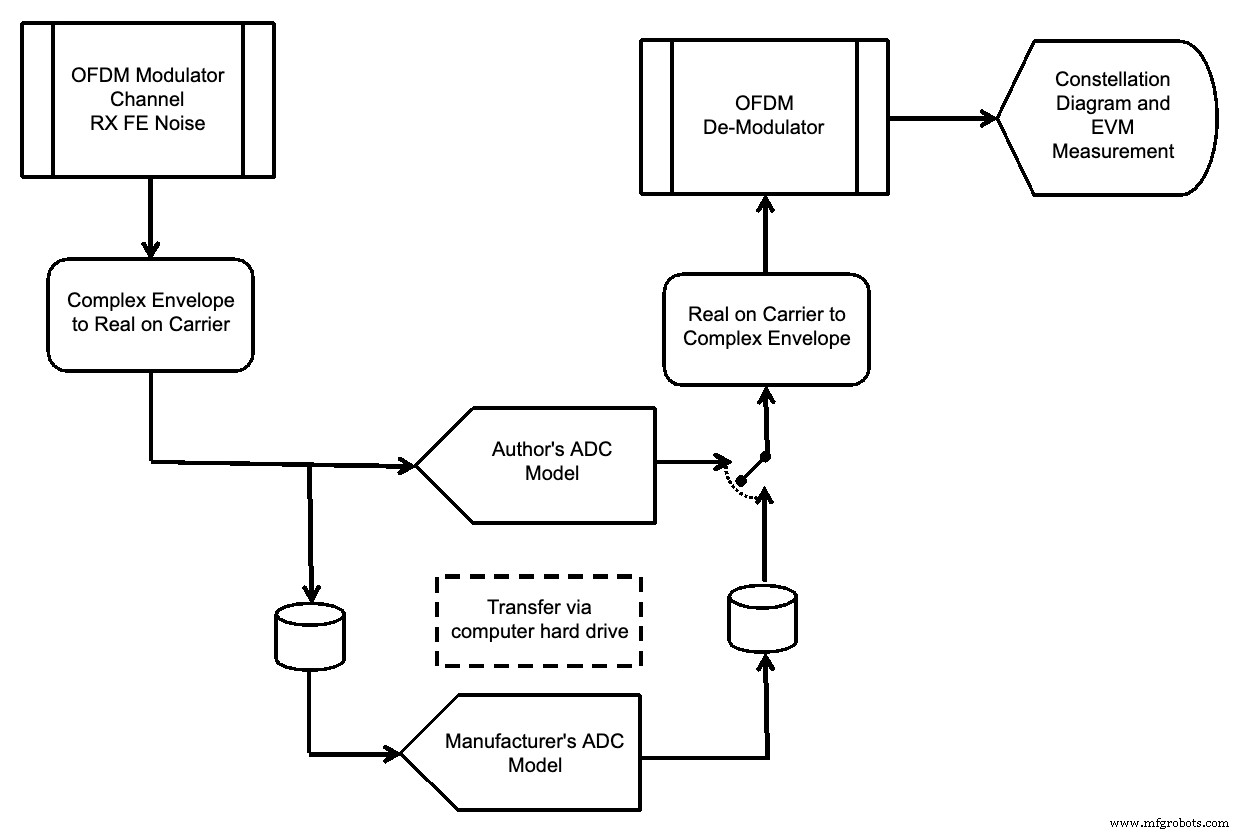
Рисунок 11.

Использовался сигнал OFDM, который имел поднесущие 64-QAM. Параметры модели АЦП, созданной вашим автором, такие же, как на рисунке 10.

В коммерчески доступном программном пакете для формирования сигналов используется сложная нотация огибающей [3]. Это позволяет отслеживать от выборки к выборке комплексными числами только информацию о модуляции, а несущую частоту просто сохранять как известную константу. Таким образом, количество выборок, необходимых для описания формы сигнала, значительно сокращается.

Однако входные данные для моделей АЦП должны быть реальным сигналом на явной несущей, чтобы учесть разницу в характеристиках АЦП в зависимости от входной частоты. Таким образом, необходимо было выполнить преобразования «Комплексная огибающая в вещественное число по несущей» и «Из действительного по несущей в комплексный конверт» [3].

На рисунке 12 показан входной сигнал OFDM для обеих моделей АЦП. Он сосредоточен на той же частоте, что и двухтональный сигнал, показанный на рисунке 8.

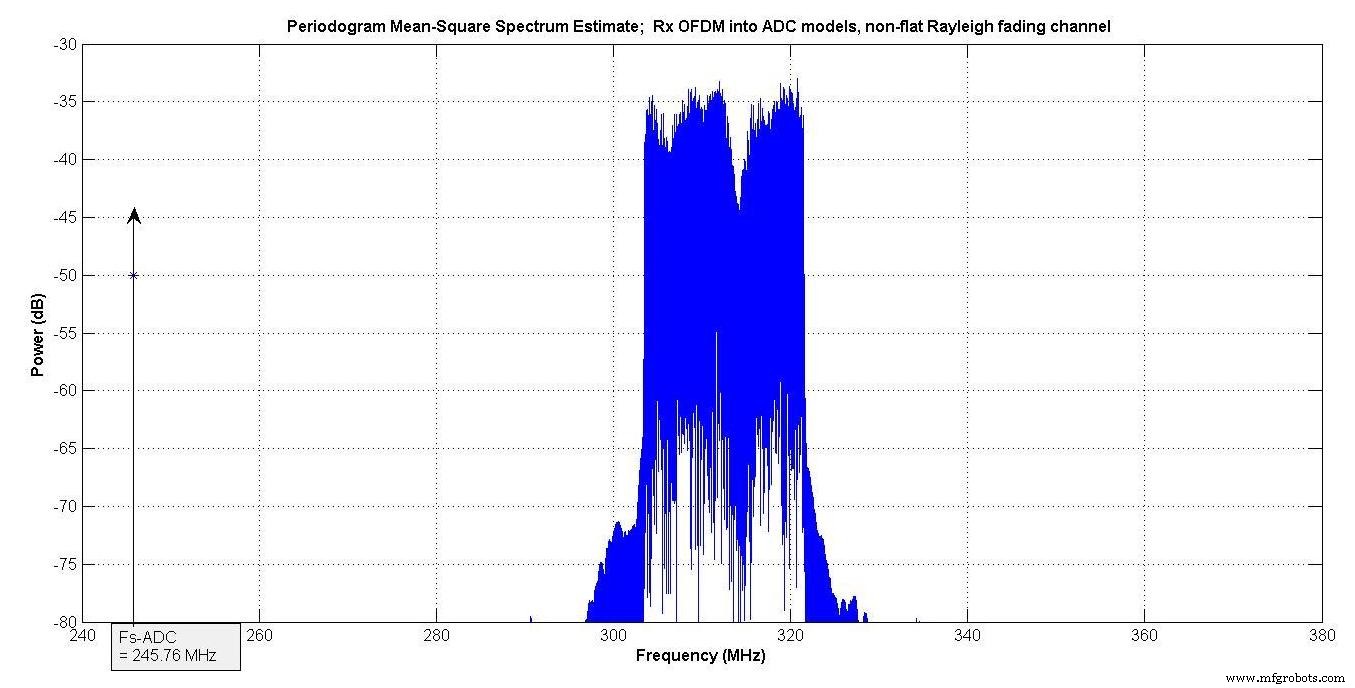
Рис. 12.

Уровень dBrmsFS в обеих моделях АЦП составлял -7 dBrmsFS.

На Рисунке 13 показан спектр модели производителя, а на Рисунке 14 - вашей авторской модели. Оба показывают рост спектра из-за нелинейности АЦП. Спектры очень близки.

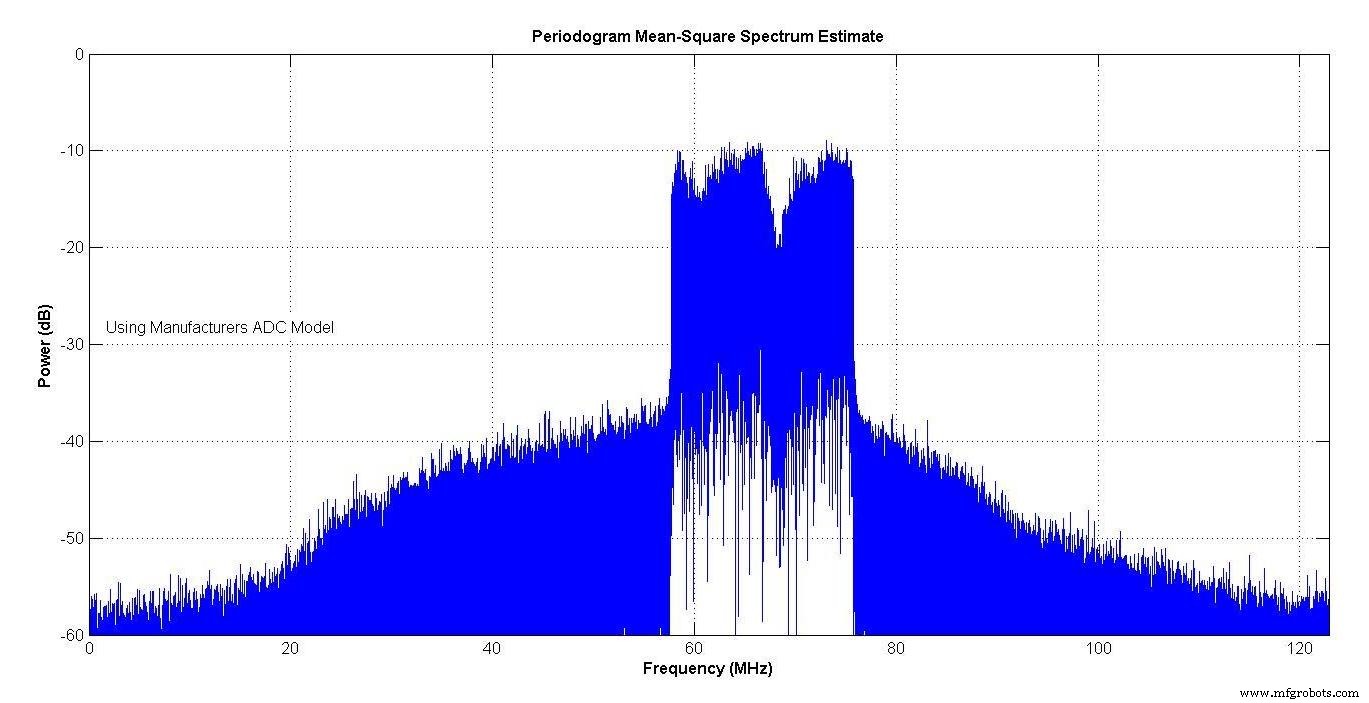
Рисунок 13

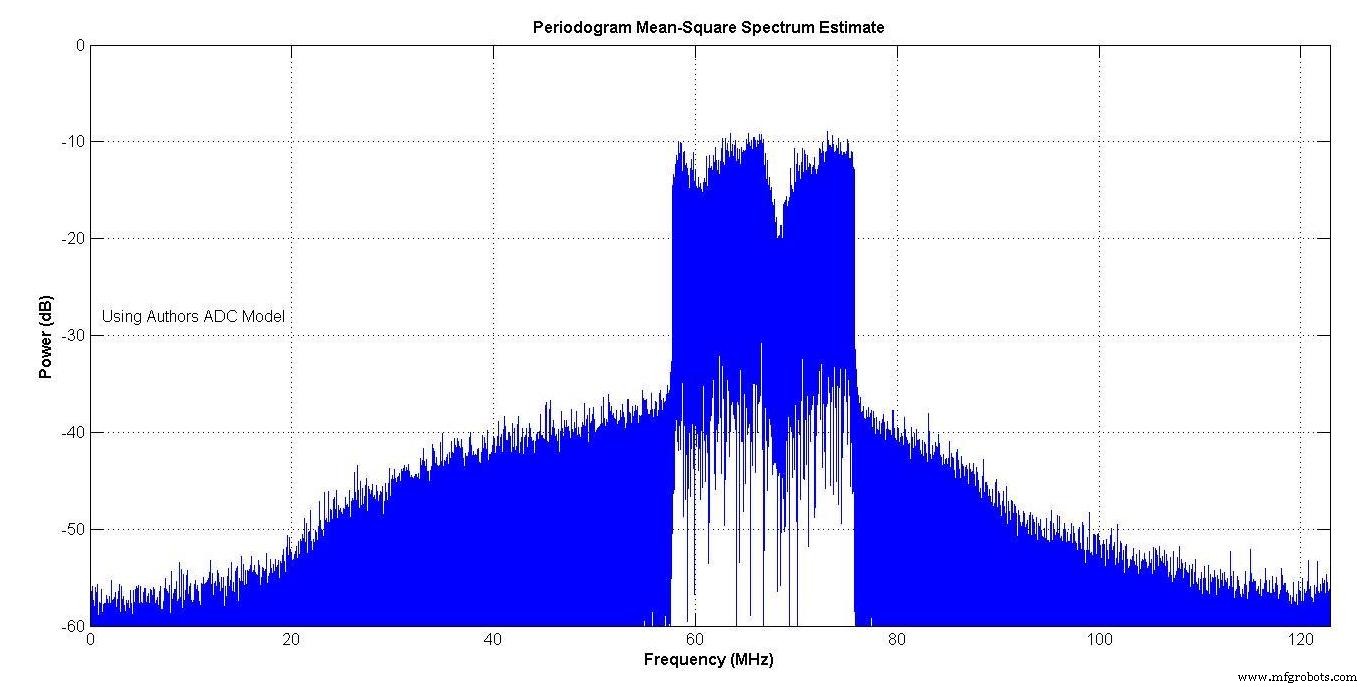
Рисунок 14.

На рисунке 15 показано совокупность полученных OFDM для модели производителя, а на рисунке 16 - для модели вашего автора.

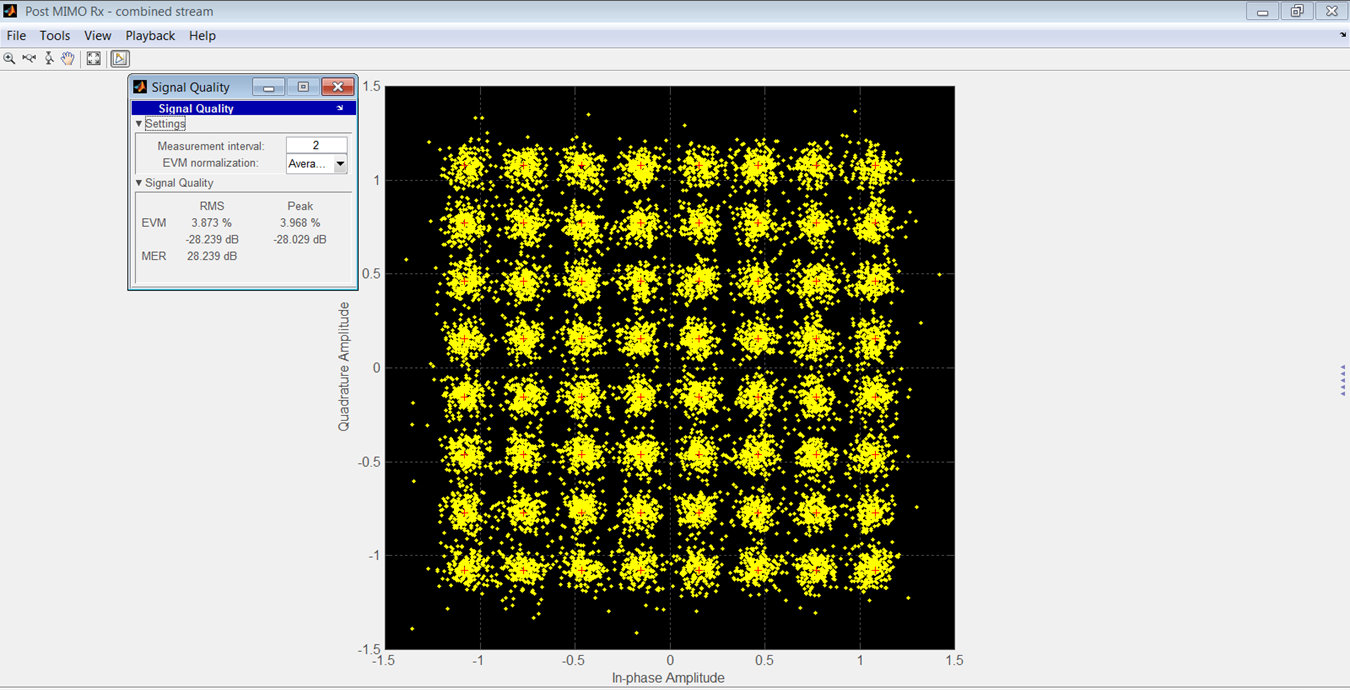
Рисунок 15.

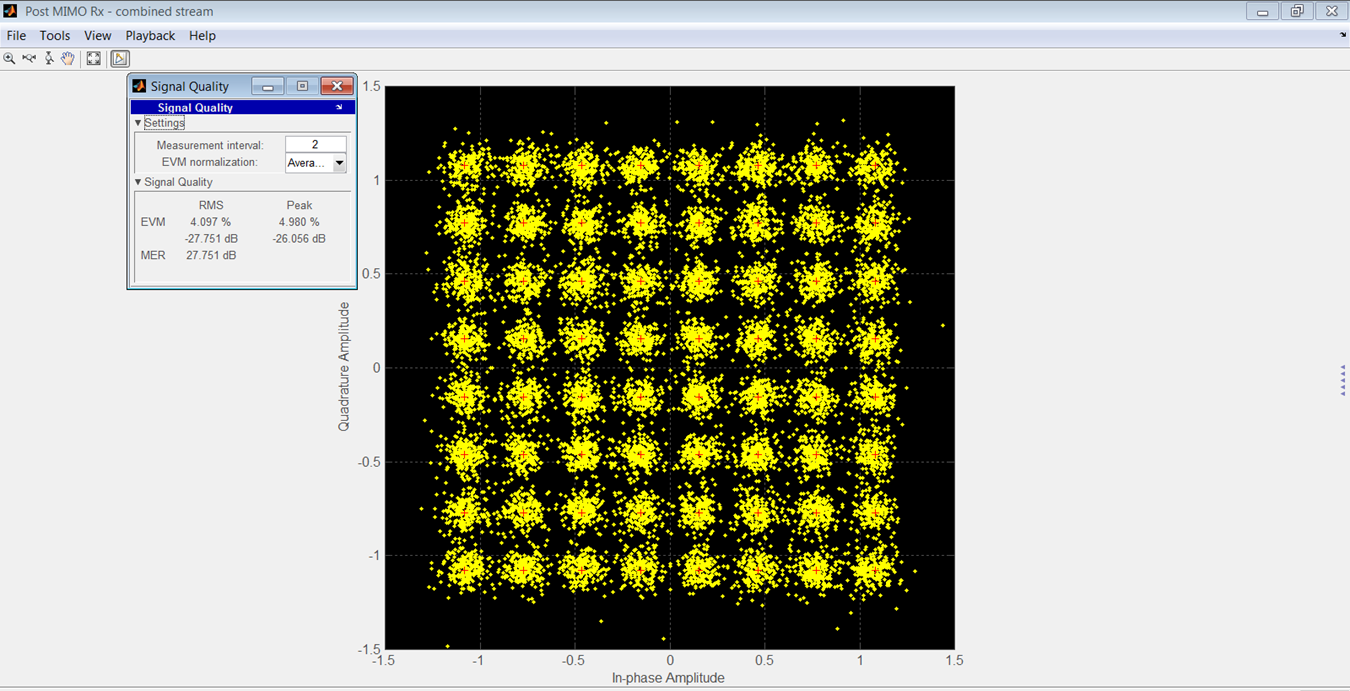
Рисунок 16.

Сравнение среднеквадратичных и пиковых значений EVM приведено в таблице 3. SNR для этих результатов составило 90 дБ.

Таблица 3.

В диапазоне от -7 до -47 дБ СКЗ среднеквадратичная разница между значениями EVM двух моделей составила 3,46 дБ.

В целом модель вашего автора дает очень похожие результаты, как и модель производителя, по довольно простому набору параметров. Информации о модели производителя не было, но она может быть похожа на авторскую.

В любом случае, моделирование выполнялось быстрее при использовании вашей авторской модели, потому что не было необходимости передавать данные между программами моделирования. Итак, модель вашего автора использовалась при моделировании коэффициента ошибок по битам (BER), показанном на рисунке 17.

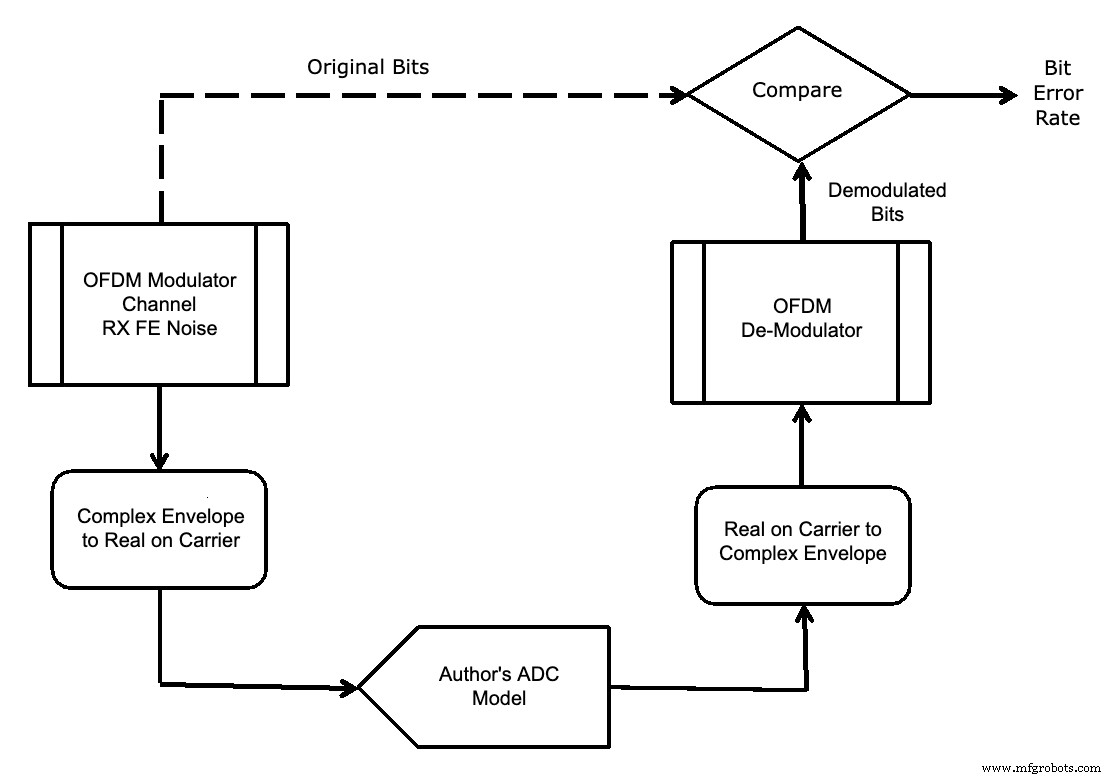
Рисунок 17.

Одним из важных параметров при разработке системы с АЦП является оптимальный уровень для размещения сигнала относительно полной шкалы АЦП.

Слишком низкий уровень приводит к тому, что сигнал становится слишком слабым по сравнению с шумом и искажениями.

Слишком высокий уровень приводит к чрезмерному ограничению, которое также искажает сигнал. Обычно оптимальным является уровень, допускающий некоторое отсечение.

BER для трех различных SNR и уровней сигнала от -41 до -7 dBrmsFS показан на рисунке 18.

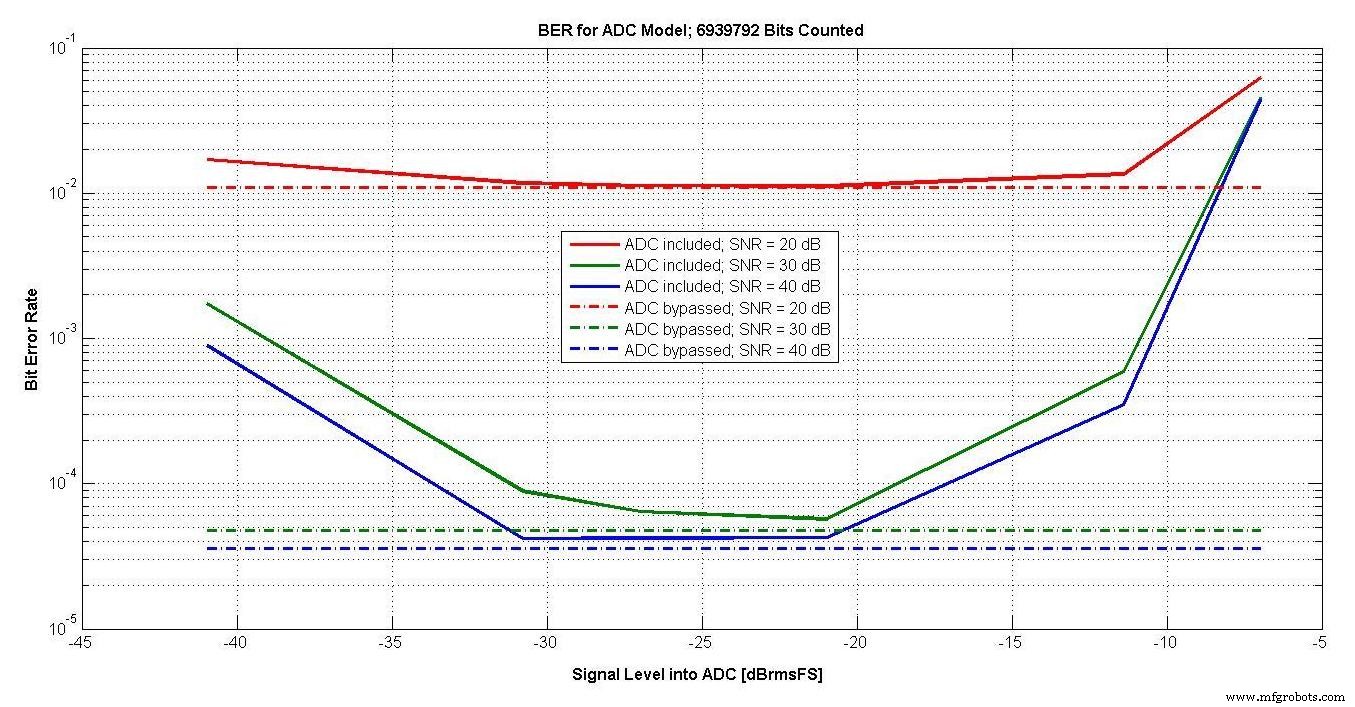
Рис. 18.

Пунктирными линиями также показан BER при обходе модели АЦП. Для АЦП диапазон порядка 10 дБ является оптимальным, и автоматическая регулировка усиления должна удерживать сигнал в этом диапазоне.

<час />

В следующей статье мы завершим эту серию некоторыми мыслями о лучшей модели для использования, а также немного поговорим о моделях для ЦАП. Поделитесь своими мыслями об этой серии в комментариях ниже.