Вычисление быстрых преобразований Фурье на микроконтроллере LPC55S69

В этой статье исследуется механизм преобразования, другая часть PowerQuad, которая позволяет микроконтроллеру LPC55S69 вычислять быстрое преобразование Фурье (БПФ).

Микроконтроллер NXP LPC55S69 содержит множество функций, которые делают его пригодным для различных приложений. Микроконтроллер LPC55S69 и его блок PowerQuad включают уникальные компоненты - Biquad и Transform Engine, которые используются для выполнения различных задач, оставляя основные ядра ЦП свободными для других задач.

В предыдущей статье «Понимание цифровой фильтрации со встроенными микроконтроллерами» были изучены различные широко используемые методы фильтрации и обработки выборок данных во временной области. Для этого он использовал двигатель Biquad блока PowerQuad LPC55S69.

В этой статье исследуется механизм преобразования, еще одна часть PowerQuad, который позволяет микроконтроллеру LPC55S69 вычислять быстрое преобразование Фурье (БПФ).

Что такое дискретные преобразования Фурье

При повседневных измерениях, таких как длина и температура, существует набор инструментов для определения размера и температуры конкретного объекта измерения. Для сигналов во временной области выбор измерительного инструмента может быть не таким очевидным. Рассмотрим следующий пример сигнала, показанный на рисунке 1.

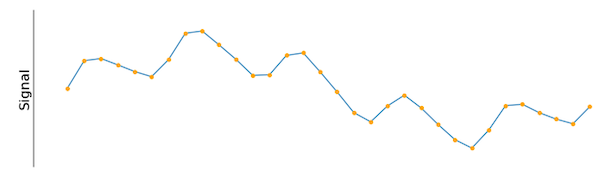
Рисунок 1. Входной сигнал, дискретизируемый с постоянным интервалом.

Как можно измерить, понять и описать этот сигнал? Возможный выбор - это амплитуда, частота или несколько значений, рассчитанных с помощью статистических методов. Один из способов начать - сопоставить интересующий сигнал с известной косинусоидальной волной, показанной на рисунке 2.

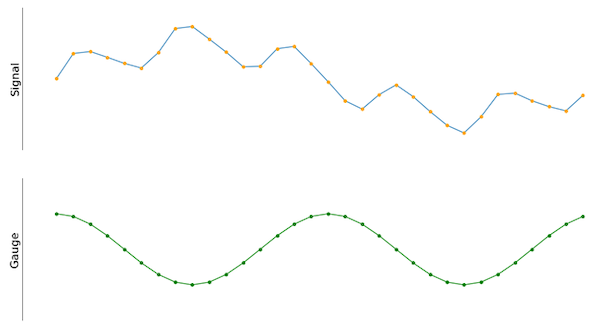
Рисунок 2. Входной сигнал рядом с сигналом косинусоидального датчика. У обоих одинаковое количество образцов.

Поскольку амплитуду и частоту косинусоидальной волны можно легко зафиксировать и, следовательно, идентифицировать, можно сравнить косинусоидальную волну с входным сигналом. Если все сделано правильно, результирующее значение скалярного произведения между входным сигналом и косинусоидальной волной количественно определяет, насколько входной сигнал коррелирует с датчиком. Для этого разумно рассматривать входной и измерительный сигнал как дискретные входные массивы одинаковой длины, и становится легко вычислить скалярное произведение.

Результатом является скаляр, величина которого пропорциональна тому, насколько хорошо входной сигнал коррелирует с сигналом косинусоидального датчика. Операция скалярного произведения сводится к множеству операций умножения и сложения - той же операции, описанной в разделе «Общие сведения о цифровой фильтрации со встроенными микроконтроллерами».

Этот метод быстро дает хорошие результаты. Однако есть частный случай, когда этот метод не работает. Если входной сигнал представляет собой косинусоидальную волну с той же частотой, что и датчик, но с фазой, сдвинутой на 90 градусов относительно датчика, выходной сигнал вышеупомянутого метода будет равен нулю. При визуальном осмотре выясняется, что корреляция между датчиком и входным сигналом все еще существует, но есть детали, которые нам необходимо учитывать.

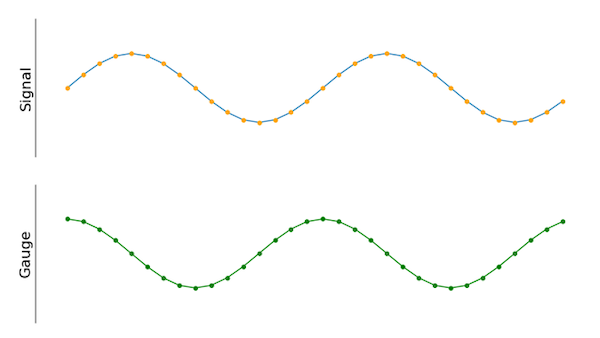
Рисунок 3. Сигнал нового датчика сдвинут по фазе на 90 градусов по сравнению со старым.

Это поведение можно сравнить с измерением «длины» тонкой полосы бумаги. При использовании линейки для определения длины одной стороны бумажной полоски бумага может быть 10 дюймов в длину и один дюйм в ширину. Оба числа верны, но для получения обоих измерений необходимо было повернуть линейку на 90 градусов. Оба числа технически верны, и мы можем использовать их вместе, чтобы получить истинный «размер» (длину и ширину) нашего листа бумаги. Чтобы решить эту проблему с точки зрения нашего входного сигнала, можно использовать второй датчик, как показано на рисунке 4.

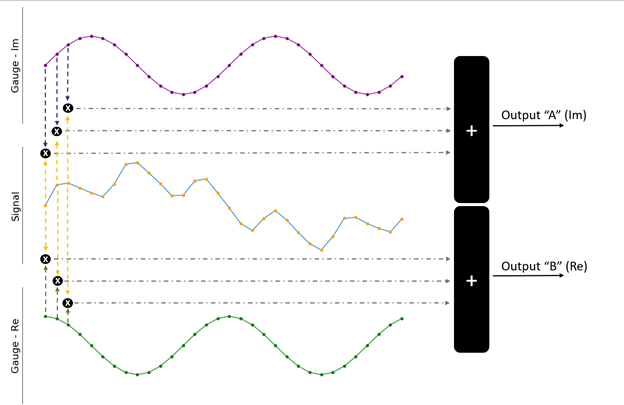
Рисунок 4. Оба сигнала датчиков можно использовать для более точной количественной оценки входного сигнала.

Единственная разница между двумя датчиками (показаны фиолетовым и зеленым) - это фазовый сдвиг на 90 градусов. В предыдущей аналогии это эквивалент вращения линейки. Скалярное произведение вычисляется между входным сигналом и каждым из датчиков для получения окончательного результата. В результате получаются два значения A и B, каждое из которых показывает, насколько хорошо входной сигнал коррелирует с одним из датчиков. Обычно они рассматриваются как одно комплексное число:

output =B + i * A

Следующим шагом является сравнение входного сигнала с диапазоном датчиков с разными частотами (рис. 5).

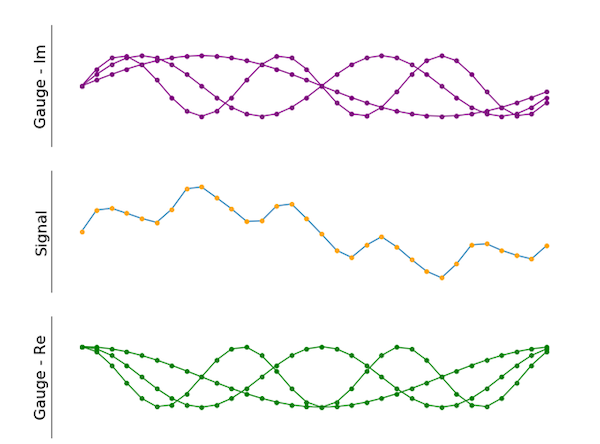
Рисунок 5. Также можно использовать несколько датчиков. Зеленые смещены на 90 градусов по сравнению с фиолетовыми.

Как показано на изображении, окончательный результат включает несколько различных датчиков. Мнимая часть (показанная фиолетовым цветом) сдвинута по фазе на 90 градусов по сравнению с зелеными сигналами (действительная часть), как и в примере с двумя датчиками, показанном выше. Количество различных датчиков не ограничено.

Использование этого метода, называемого дискретным преобразованием Фурье (ДПФ), позволяет генерировать спектр выходных сигналов на всех частотах, представляющих интерес для задачи. Математически эту технику можно сформулировать следующим образом:

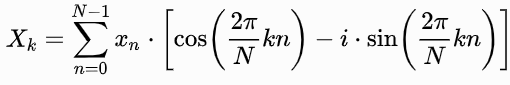
Уравнение 1. Математическое описание ДПФ.

Где N - количество выборок во входном сигнале, а k - частота (со) эталонных синусоидальных датчиков.

Ограничения быстрого преобразования Фурье (БПФ)

БПФ - это численно эффективный способ вычисления ДПФ, который требует меньшего количества операций умножения и сложения по сравнению с методом, описанным выше. Однако есть несколько ограничений на ввод:

1. Длина входных данных должна быть степенью двойки.
2. Произвольная длина ввода и частотный интервал на выходе не допускаются. Выходные ячейки разделены частотой дискретизации входного сигнала, деленной на количество выборок на входе. Если входной сигнал представляет собой, например, 256-точечный сигнал, дискретизированный с частотой 48 кГц, выходные массивы соответствуют частотам, разнесенным с интервалом 187 Гц (48,000, разделенные на 256).
3. Когда входные данные состоят из действительных чисел (например, выборки, полученные от АЦП), выходные данные симметричны. Если вход, например, состоит из 64 отсчетов, результат БПФ также будет состоять из 64 комплексных чисел. Однако вторая половина выходного массива содержит комплексные конъюгаты первой половины.

Использование механизма PowerQuad FFT

Математика, лежащая в основе операций ДПФ / БПФ, может выполняться с помощью простых операций умножения и сложения, что идеально подходит для передачи математических операций на аутсорсинг специализированному сопроцессору, например PowerQuad на микроконтроллере LPC55S69. Благодаря этому основные ядра ЦП могут работать над другими задачами.

Использование механизма PowerQuad FFT - простой процесс, и официальный SDK поставляется с примерами проектов, демонстрирующих функции совместной обработки. В частности, один пример, называемый powerquad_transform, демонстрирует процесс вычисления БПФ.

Файл powerquad_transform.c содержит несколько функций, которые проверяют различные режимы механизма БПФ. Одна из них - функция PQ_RFFTFixed16Example. В этом примере PowerQuad инициализируется для приема 16-разрядных целочисленных данных. Данные с плавающей запятой необходимо предварительно преобразовать в значения с фиксированной запятой, поскольку механизм преобразования PowerQuad поддерживает только целые числа.

FILTER_INPUT_LEN определяет количество входных выборок. Выходной массив вдвое длиннее, потому что он должен хранить действительную и мнимую части результирующих значений.

Рисунок 6. Эта часть кода определяет тестовые данные и ожидаемые результаты.

Последний массив содержит тестовые данные для проверки результата. Обратите внимание, как вторая половина массива содержит комплексные конъюгаты, как указано выше. Кроме того, конъюгаты не равны (например, пара 76, -50 и 77,49). В любом случае, после инициализации данных для настройки PowerQuad используется следующая структура данных:

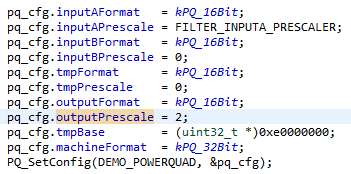
Рисунок 7. В этой части примера программы выполняется настройка и инициализация модуля PowerQuad.

Необходимо уменьшить масштаб ввода, чтобы алгоритм не переполнялся. Этот процесс происходит во второй строке на изображении выше. FILTER_INPUTA_PRESCALER установлен в пять, потому что есть 32 (два в степени пяти) выборки. Предварительное масштабирование - это еще одна аппаратная функция PowerQuad, которая, вероятно, является причиной неточности, наблюдаемой в ожидаемых результатах тестирования.

После того, как все настроено, расположение областей ввода и вывода передается модулю PowerQuad, что происходит в функции PQ_transformRFFT. Этот метод устанавливает несколько регистров конфигурации и запускает PowerQuad, записывая данные в регистр управления. В этом примере ЦП ожидает завершения PowerQuad. Ожидание не всегда необходимо, и PowerQuad может выполнять вычисления асинхронно, в то время как ЦП выполняет другие задачи.

Используйте PowerQuad для математических операций

PowerQuad - это сопроцессор для сложных математических операций, доступный на различных устройствах серии MCU LPC5500. Он включает в себя специальный механизм для эффективного вычисления БПФ, который может выполняться независимо от основных ядер ЦП. SDK для микроконтроллера LPC55S69 содержит примеры настройки и использования PowerQuad.

Страница сообщества NXP содержит обширную информацию, обсуждения и статьи, посвященные микроконтроллеру LPC55S69.

Отраслевые статьи - это форма контента, позволяющая отраслевым партнерам делиться полезными новостями, сообщениями и технологиями с читателями All About Circuits, что не подходит для редакционного контента. Все отраслевые статьи подлежат строгим редакционным правилам с целью предлагать читателям полезные новости, технические знания или истории. Точки зрения и мнения, выраженные в отраслевых статьях, принадлежат партнеру, а не обязательно All About Circuits или ее авторам.