Теоремы ДеМоргана

Математик по имени ДеМорган разработал пару важных правил, касающихся дополнения групп в булевой алгебре.

По группе дополнение, я имею в виду дополнение группы терминов, представленное длинной полосой над более чем одной переменной.

Вы должны вспомнить из главы о логических вентилях, что инвертирование всех входов в вентиль меняет основную функцию этого логического элемента с И на ИЛИ или наоборот, а также инвертирует выход.

Таким образом, вентиль ИЛИ со всеми инвертированными входами (вентиль отрицательного ИЛИ) ведет себя так же, как вентиль И-НЕ, а вентиль И со всеми инвертированными входами (вентиль отрицательного И) ведет себя так же, как вентиль ИЛИ-ИЛИ.>

Теоремы ДеМоргана утверждают ту же эквивалентность в «обратной» форме:инвертирование выхода любого логического элемента приводит к той же функции, что и вентиль противоположного типа (И против ИЛИ) с инвертированными входами:

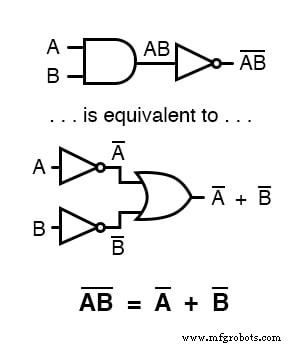
Длинная полоса, проходящая над термином AB, действует как группирующий символ и как таковая полностью отличается от независимо инвертированного произведения A и B.

Другими словами, (AB) ’не равно A’B’. Поскольку «главный» символ (’) не может быть растянут на две переменные, как столбец, мы вынуждены использовать круглые скобки, чтобы применить его ко всему термину AB в предыдущем предложении.

Однако полоса действует как отдельный символ группировки, когда растягивается более чем на одну переменную.

Как мы увидим, это оказывает глубокое влияние на то, как вычисляются и сокращаются логические выражения.

Теорема ДеМоргана

Теорема ДеМоргана может рассматриваться с точки зрения нарушения символ длинной полосы.

Когда длинный столбец сломан, операция непосредственно под разрывом меняется с сложения на умножение или наоборот, а части сломанного столбца остаются над отдельными переменными. Для иллюстрации:

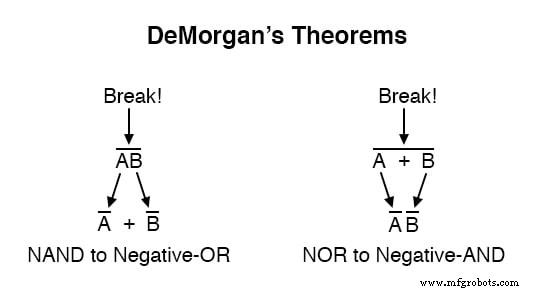
Если в выражении существует несколько «слоев» полосок, вы можете разбивать только одну полосу за раз , и обычно проще начать упрощение, сломав сначала самую длинную (самую верхнюю) полосу.

Для иллюстрации возьмем выражение (A + (BC) ’)’ и сократим его с помощью теорем ДеМоргана:

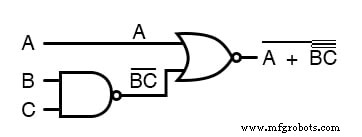
Следуя совету сначала сломать самую длинную (самую верхнюю) полосу, я начну с того, что сломаю полосу, покрывающую все выражение, в качестве первого шага:

В результате исходная схема сокращается до логического элемента И с тремя входами с инвертированным входом A:

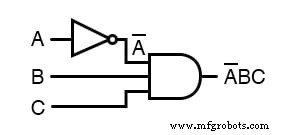
Вы не должны никогда сломать более одной полосы за один шаг, как показано здесь:

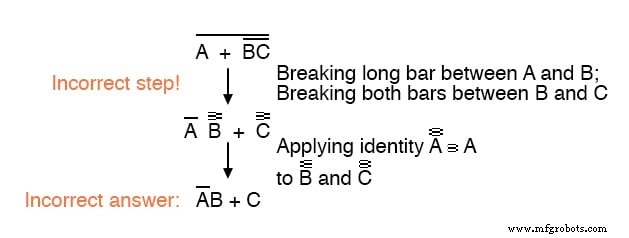
Как ни заманчиво экономить шаги и ломать более одной планки за раз, это часто приводит к неверному результату, так что не делайте этого!

Можно правильно уменьшить это выражение, сначала сломав короткую полосу, а не длинную:

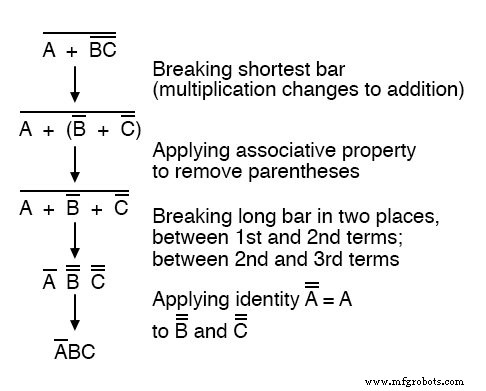
Конечный результат тот же, но требуется больше шагов по сравнению с использованием первого метода, когда самая длинная полоса ломалась первой.

Обратите внимание, как на третьем этапе мы сломали длинную планку в двух местах.

Это правильная математическая операция, а не то же самое, что сломать две планки за один шаг!

Запрет на нарушение более чем одной полосы за один шаг не запрет на разбивание планки более чем в одном месте.

Нарушение более чем в одном месте за один шаг это нормально; нарушение более чем одной планки ни за один шаг - нет.

Вам может быть интересно, почему скобки были заключены в подвыражение B ’+ C’, учитывая тот факт, что я просто удалил их на следующем шаге.

Я сделал это, чтобы подчеркнуть важный, но легко игнорируемый аспект теоремы ДеМоргана.

Поскольку длинная полоса функционирует как символ группировки, переменные, ранее сгруппированные прерывистой полоской, должны оставаться сгруппированными, чтобы не потерять надлежащий приоритет (порядок работы).

В этом примере не имело бы значения, если бы я забыл поставить скобки после того, как сломал короткую полосу, но в других случаях это могло бы быть.

Рассмотрим этот пример, начиная с другого выражения:

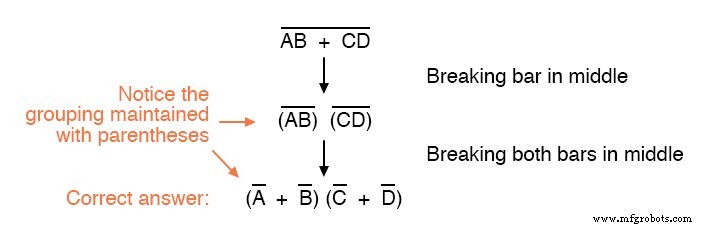
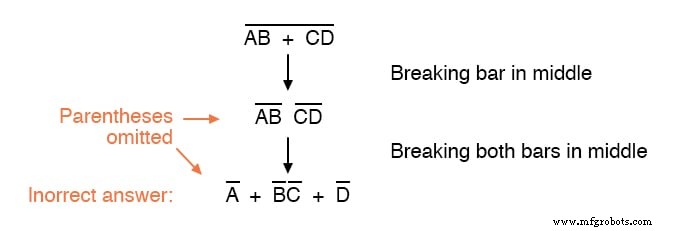
Как видите, сохранение группировки, подразумеваемой полосками дополнения для этого выражения, имеет решающее значение для получения правильного ответа.

Давайте применим принципы теорем ДеМоргана к упрощению схемы затвора:

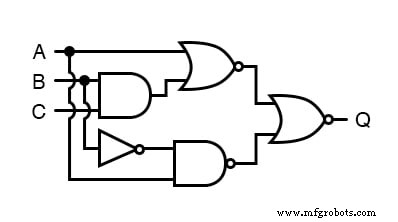
Как всегда, нашим первым шагом в упрощении этой схемы должно быть создание эквивалентного логического выражения.

Мы можем сделать это, поместив метку подвыражения на выходе каждого элемента, когда входные данные станут известны. Вот первый шаг в этом процессе:

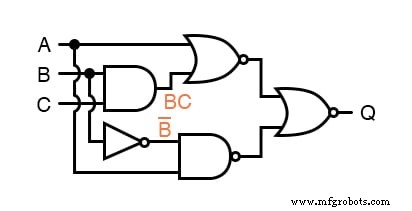
Затем мы можем пометить выходы первого логического элемента ИЛИ-НЕ и логического элемента И-НЕ.

Имея дело с вентилями с инвертированным выходом, мне легче написать выражение для выхода вентиля без последняя инверсия со стрелкой, указывающей прямо перед пузырем инверсии.

Затем у провода, ведущего из ворот (после пузыря), я пишу полное дополненное выражение.

Это помогает убедиться, что я не забуду дополняющую полосу в подвыражении, заставляя себя разделить задачу написания выражения на два этапа:

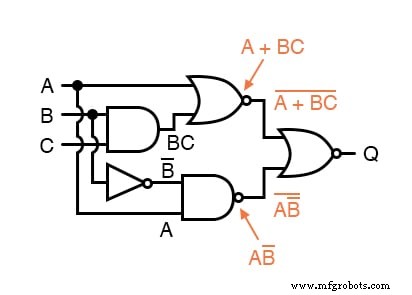
Наконец, мы пишем выражение (или пару выражений) для последнего логического элемента ИЛИ-НЕ:

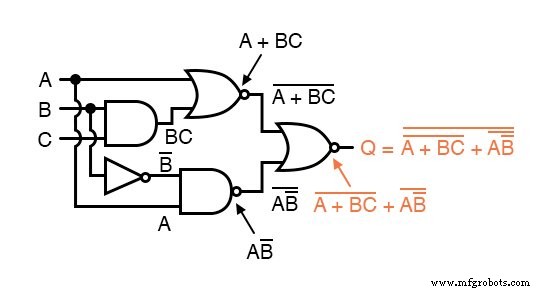
Теперь мы сокращаем это выражение, используя тождества, свойства, правила и теоремы (ДеМоргана) булевой алгебры:

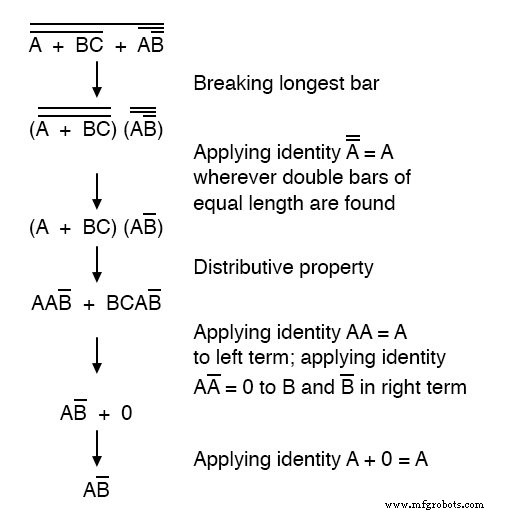
Эквивалентная схема затвора для этого значительно упрощенного выражения выглядит следующим образом:

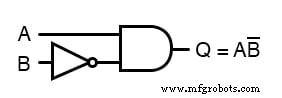
ОБЗОР:

• Теоремы ДеМоргана описывают эквивалентность между вентилями с инвертированными входами и вентилями с инвертированными выходами. Проще говоря, вентиль И-НЕ эквивалентен вентилю отрицательного ИЛИ, а вентиль ИЛИ - вентилю отрицательного И.
• При «разрыве» полосы дополнения в логическом выражении операция непосредственно под разрывом (сложение или умножение) меняется на противоположную, и части сломанной полосы остаются над соответствующими терминами.
• Часто бывает проще решить проблему, сломав самую длинную (самую верхнюю) полосу, прежде чем разбивать какие-либо полосы под ней. Вы не должны никогда попытаться сломать две планки за один прием!
• Полосы дополнения работают как символы группировки. Следовательно, когда столбец сломан, термины под ним должны оставаться сгруппированными. Эти сгруппированные термины можно заключить в круглые скобки, чтобы избежать изменения приоритета.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

• Рабочий лист булевой алгебры